포드-풀커슨 알고리즘(최대 유량 문제)
🌟 최대 유량 문제(=네트워크 플로우)
특정한 지점에서 다른 지점으로, 얼마나 많은 유량을 동시에 보낼 수 있는지 계산하는 문제
✏️ 용어 정리
용량 : c(u,v)
정점 u에서 v로 전송할 수 있는 최대 용량
유량 : f(u,v)
정점 u에서 v로 실제 흐르고 있는 유량
잔여 용량 : r(u,v) = c(u,v) - f(u,v)
간선의 용량과 실제로 흐르는 유량의 차이
소스 s
모든 유량이 시작되는 정점
싱크 t
모든 유량이 도착하는 정점
증가 경로
소스에서 싱크로 유량을 보낼 수 있는 경로
✏️ 기본 속성
용량 제한 속성 f(u,v) <= c(u,v)
유량은 용량보다 작거나 같다.
유량의 대칭성 f(u,v) = -f(v,u)
u에서 v로 유량이 흐르면, v에서 u로 음수의 유량이 흐르는 것과 동일하다.
유량의 보존성
각 정점에 들어오는 유량과 나가는 유량은 같다.
🌟 기존 최대 유량 탐색 방법의 문제점

프로그램은 S에서 T로 가는 모든 경로를 탐색하며, 최대 유량을 계산할 것이다.
S 👉 a 👉 T
S 👉 a 👉 b 👉 T
S 👉 b 👉 T
만약, 프로그램이 아래 그림과 같이 S→a →T와 S →b →T의 경로를 먼저 탐색하게 된다면
해당 네트워크의 최대 유량은 2가 되면서 프로그램은 정답을 맞추게 된다.

하지만, 만약 프로그램이 아래 그림과 같이 S→a →b →T의 경로를 가장 먼저 탐색하게 되면
S → a, a → b, b →T 간선의 유량이 최대치이기 때문에
S → b 에 추가로 연결된 경로를 찾지 못하게 되고
최대 유량이 1인 상태에서 프로그램은 중지되게 된다.

👉 유량 상쇄를 통해 문제 해결 가능
🌟 유량 상쇄
모든 경로에, 기존에 존재하는 간선들과 반대되는 방향의 간선을 추가한 뒤
각 간선으로 유량을 흘려보냈을 때, 반대 방향의 간선으로도 음의 유량을 흘려보냄으로써, 유량을 상쇄시키는 것
물론, 실제로는 불가능한 이야기이지만, 음의 유량을 기록함으로써 잔여 용량을 남겨, 추가적인 경로를 탐색할 수 있도록 하기 위함이다.
EX
a → b의 간선이 존재하며, 유량 f(a,b)은 1, 용량 c(a,b)은 1이라면
역간선 b → a의 유량 f(b,a)은 기존 간선의 방향과 반대이므로 -1이 되며
용량 c(b,a)은 실제 존재하는 간선이 아니므로 0이 된다.
따라서, 역간선 b → a의 잔여 용량 r(b,a)은 c(b,a) - f(b,a) = 0 - (-1) = 1이 된다.
즉, 역간선 b → a로 1의 유량을 추가적으로 흘려보낼 수 있게 된다.
👉 해당 규칙은 두 정점이 서로에게 유량을 보내주는 것이 의미가 없기 때문에 성립할 수 있으며, 소스에서 싱크로 가는 총 유량도 변하지 않는다.
🟩 포드-풀커슨 알고리즘
1. 네트워크에 존재하는 모든 간선의 유량을 0으로 초기화하고, 역방향 간선의 유량도 0으로 초기화한다.
2. 소스에서 싱크로 갈 수 있는, 잔여 용량이 남은 경로를 DFS로 탐색한다.
3. 해당 경로에 존재하는 간선들의 잔여 용량 중, 가장 작은 값을 유량으로 흘려보낸다.
4. 해당 유량에 음수값을 취해, 역방향 간선에도 흘려보낸다 (유량 상쇄)
5. 더 이상 잔여 용량이 남은 경로가 존재하지 않을 때까지 반복한다.
🟩 예제

위 그림은, 네트워크에 존재하는 모든 간선의 유량을 0으로 초기화시키고, 역방향 간선의 유량도 0으로 초기화한 뒤
DFS를 통해, 소스에서 싱크로 갈 수 있는 경로 중 하나인 S → a → b → T 경로를 탐색하고
해당 경로에 존재하는 간선들의 잔여 용량 중, 가장 작은 값인 1을 유량으로 흘려보낸 뒤
해당 유량에 음수값을 취해, 역방향 간선에도 -1을 흘려보낸 결과이다.
즉, b에서 a로 1만큼의 유량을 추가로 흘려보낼 수 있는 것을 알 수 있다.
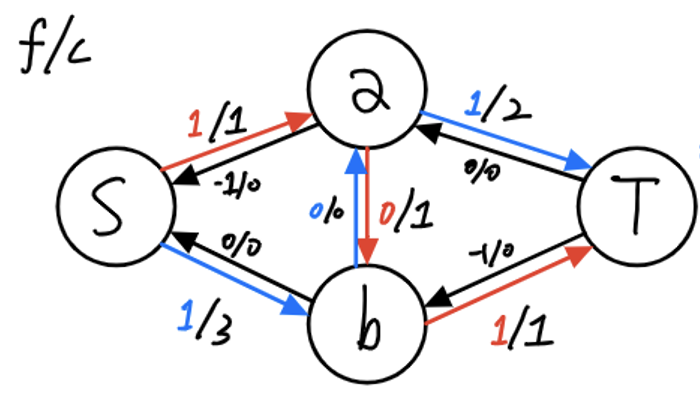
결과적으로, 간선 (a,b)와 (b,a)가 상쇄되므로, 아래와 같은 정답이 도출된다.
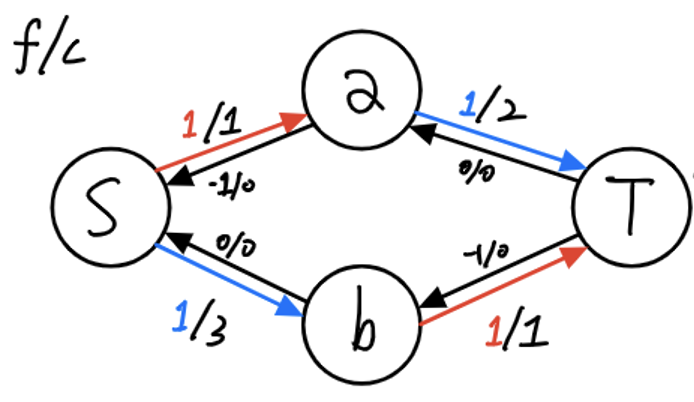
🟩 특징
DFS 방식으로 증가 경로를 찾는다.
비효율적으로 동작 가능 cf. 문제의 최대 유량이 적고, 간선이 많으면 오히려 DFS가 효율적일 수 있다.
시간복잡도 O((E+V) * F)
